Dony :)

FE로 성장 중 🌱

선택 정렬이란?

(오름차순 기준)

  • 버블 정렬과 비슷하지만 큰 값을 먼저 배열의 끝에 위치시키는게 아니라 작은 값을 하나씩 자리에 정렬시키는 방법이다.
  • 내부 for문이 앞에서 뒤까지 움직이는 것은 같지만, 실제로 정렬되는 데이터는 앞에서 축적된다.

정렬 방법

  1. 첫 번째 원소를 초기 최솟값으로 저장한다.
  2. 더 작은 숫자를 찾을 때까지 이 최솟값을 배열의 다음 항목들과 비교한다.
  3. 더 작은 숫자를 찾으면 더 작은 숫자를 새로운 최솟값으로 지정하고 배열이 끝날 때까지 계속한다.
  4. 최솟값이 처음에 시작했던 값이 아닌 경우 두 값을 바꾼다.
  5. 배열이 정렬될 때까지 다음 요소에서도 이 작업을 반복한다.

정렬 알고리즘 예시 시각화 사이트: https://visualgo.net/en/sorting

< 예시 >

선택 정렬 설명 이미지
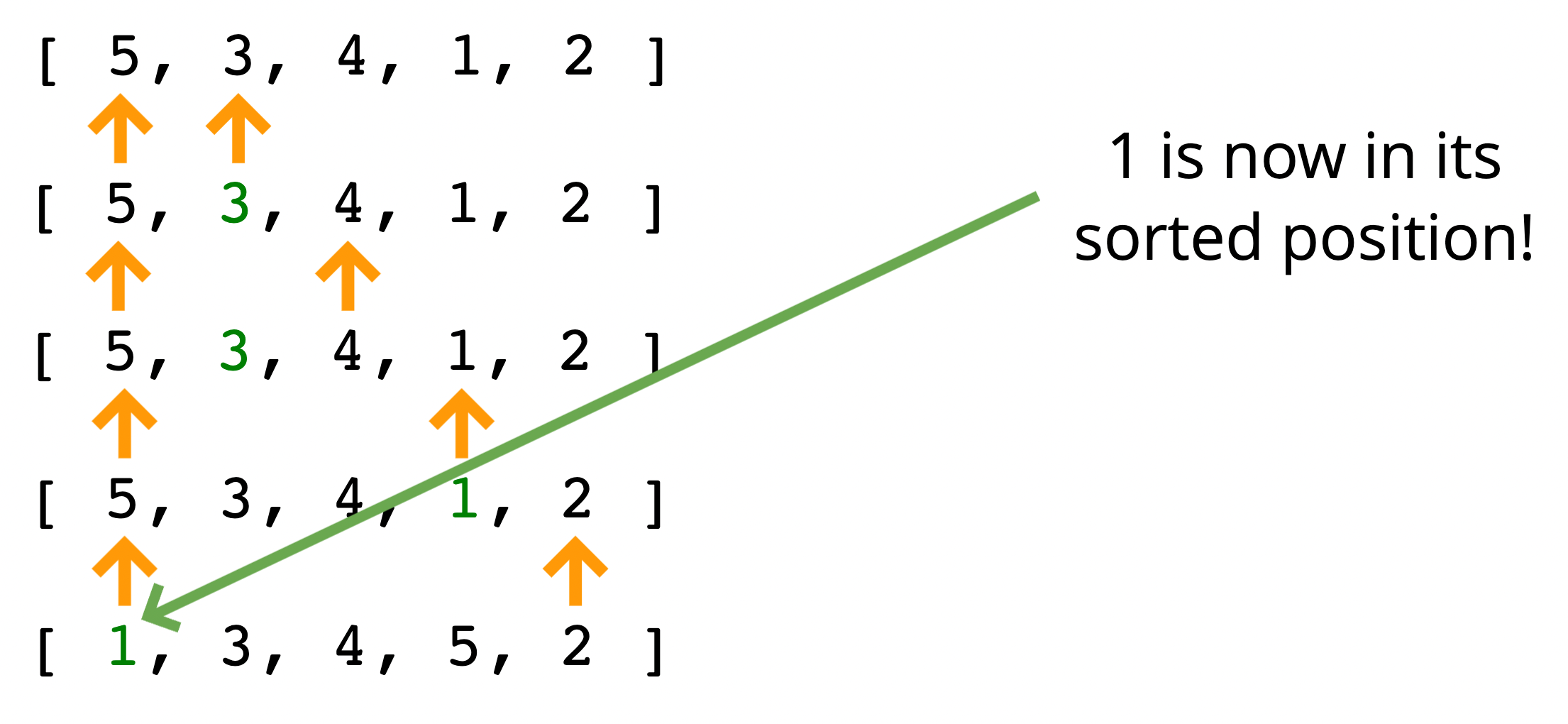
위의 예시 이미지를 보면
첫 번째 화살표는 지정한 시작점(내부 for문의 시작 index)이고, 두번 째 화살표는 비교 대상이다.
초록색 숫자는 순회하면서 현재 최솟값을 의미한다.

  1. 초기 최솟값으로 되있는 5와 3을 비교한다.
    3이 더 작다. 그러면 3이 현재 최솟값이 된다.
  2. 3과 4를 비교한다.
    여전히 3이 더 작다.
  3. 3과 1을 비교한다.
    이번에는 1이 작다. 1이 새로운 최솟값이 된다.
  4. 1과 2를 비교한다.
    여전히 1이 더 작다.
  5. 이제 마지막에 도착했으니 자리 바꾸기를 한다.
    최솟값인 요소를 첫 번째 화살표의 요소와 자리 바꾸기를 한다.
    그럼 배열에 있는 가장 작은 요소가 맨 앞으로 가게 된다.

이것이 한번 순회하는 과정이다.

선택 정렬 구현

그럼 이제 선택 정렬을 구현해보자.

function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let lowest = i; // 최솟값이 들어올 지점

    for (let j = i + 1; j < arr.length; j++) {
      // 최솟값과 다음 요소를 비교하기 위해 i+1부터 시작
      console.log(arr, arr[i], arr[lowest], arr[j]);
      if (arr[j] < arr[lowest]) {
        // 현재 값이 현재 최솟값보다 작을 경우
        lowest = j; // 그 index를 재할당
      }
    }

    if (i !== lowest) {
      // 최솟값이 처음에 시작했던 값이 아닌 경우
      [arr[i], arr[lowest]] = [arr[lowest], arr[i]]; // 시작 지점의 값과 최솟값을 swipe
      console.log(arr + " <= swipe");
    }
    console.log("=====================================================");
  }

  return arr;
}

selectionSort([0, 2, 34, 22, 10, 19, 17]);

//            arr                i   arr[lowest]  arr[j]
// [0, 2, 34, 22, 10, 19, 17]    0        0         2
// [0, 2, 34, 22, 10, 19, 17]    0        0         34
// [0, 2, 34, 22, 10, 19, 17]    0        0         22
// [0, 2, 34, 22, 10, 19, 17]    0        0         10
// [0, 2, 34, 22, 10, 19, 17]    0        0         19
// [0, 2, 34, 22, 10, 19, 17]    0        0         17
// =====================================================
// [0, 2, 34, 22, 10, 19, 17]    1        2         34
// [0, 2, 34, 22, 10, 19, 17]    1        2         22
// [0, 2, 34, 22, 10, 19, 17]    1        2         10
// [0, 2, 34, 22, 10, 19, 17]    1        2         19
// [0, 2, 34, 22, 10, 19, 17]    1        2         17
// =====================================================
// [0, 2, 34, 22, 10, 19, 17]    2        34        22
// [0, 2, 34, 22, 10, 19, 17]    2        22        10
// [0, 2, 34, 22, 10, 19, 17]    2        10        19
// [0, 2, 34, 22, 10, 19, 17]    2        10        17
// [0, 2, 10, 22, 34, 19, 17] <= swipe
// =====================================================
// [0, 2, 10, 22, 34, 19, 17]    3        22        34
// [0, 2, 10, 22, 34, 19, 17]    3        22        19
// [0, 2, 10, 22, 34, 19, 17]    3        19        17
// [0, 2, 10, 17, 34, 19, 22] <= swipe
// =====================================================
// [0, 2, 10, 17, 34, 19, 22]    4        34        19
// [0, 2, 10, 17, 34, 19, 22]    4        19        22
// [0, 2, 10, 17, 19, 34, 22] <= swipe
// =====================================================
// [0, 2, 10, 17, 19, 34, 22]    5        34        22
// [0, 2, 10, 17, 19, 22, 34] <= swipe
// =====================================================

선택 정렬의 시간복잡도

선택 정렬은 버블 정렬에 비해 자리 바꾸기를 덜하기 때문에 공간복잡도 측면에서는 더 효율적이다.
그러나 시간복잡도에서는 모든 정렬이 어느정도 되어있는지를 떠나서 항상 모두 순회해야하기 때문에 효율성이 떨어진다.

  • 최악의 경우: O(n2)
    - 정렬하려는 기준의 완전 반대 경우
    ex) [4, 3, 2, 1]
  • 평균: O(n2)
  • 최고의 경우: O(n2)
  • 공간복잡도: O(1)

참고