Dony :)

FE로 성장 중 🌱

퀵 정렬이란?

  • 합병 정렬과 마찬가지로 0개 또는 1개 요소의 배열은 항상 정렬된다는 사실을 활용한다.
  • 하나의 요소(피벗(pivot))를 선택하고 정렬된 배열에서 피벗이 끝나야 하는 인덱스를 찾는 방식으로 작동한다.
  • 피벗이 적절하게 배치되면 피벗의 양쪽에 빠른 정렬을 적용할 수 있다.

퀵 정렬 방법

  1. 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
  2. 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
  3. 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
  • 분할된 리스트에 대하여 재귀 호출을 이용하여 정렬을 반복한다.
  • 분할된 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 분할된 리스트로 나누는 과정을 반복한다. (분할 리스트의 갯수가 1개 이하가 될 때까지 반복)

정렬 알고리즘 예시 시각화 사이트: https://visualgo.net/en/sorting

< 예시 >

퀵 정렬 설명

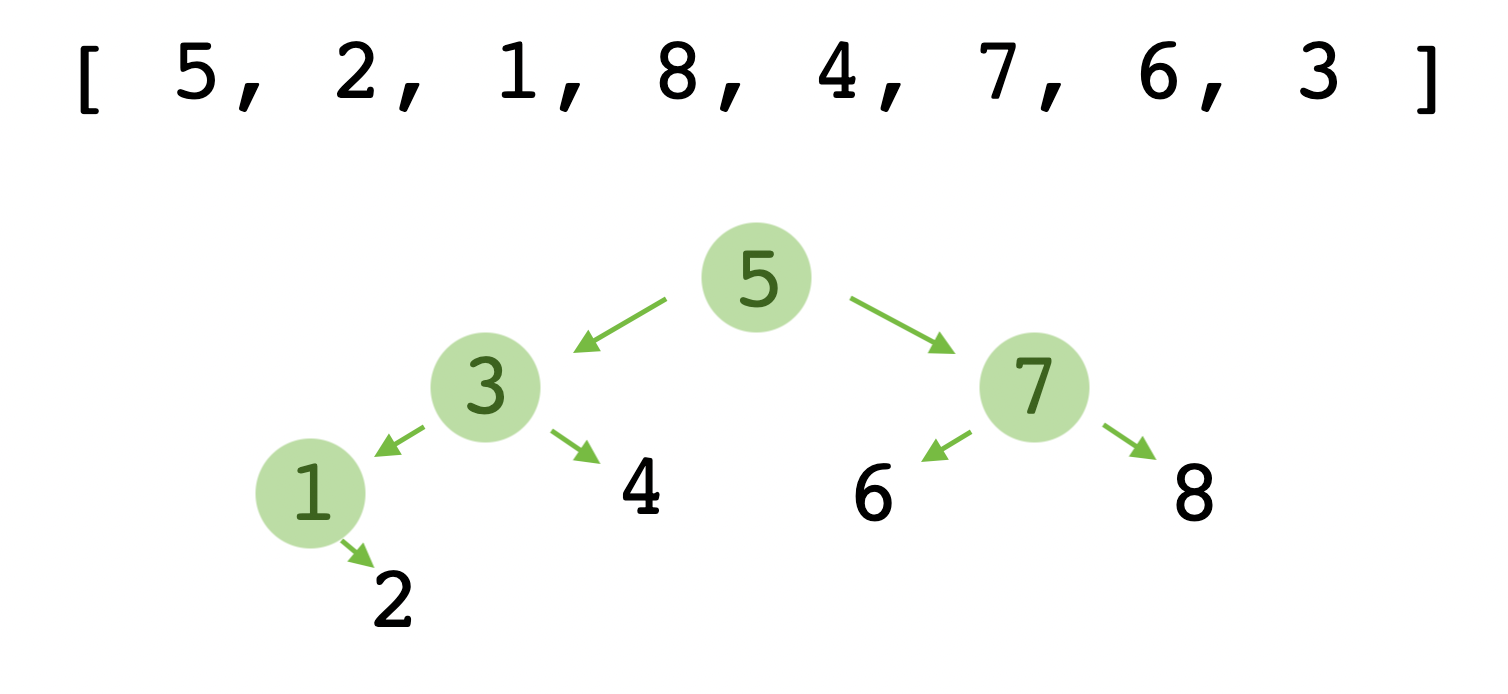
  1. 5를 선택하여 5를 기준으로 작은 숫자는 왼쪽, 큰 숫자는 오른쪽으로 나눈다.
  2. 왼쪽에서 3을 기준으로 작은 숫자는 왼쪽, 큰 숫자는 오른쪽으로 나눈다.
  3. 왼쪽에 배열크기가 1개 이하가 될 때까지 반복한다. 오른쪽도 위의 과정과 같게 반복한다.

구현하기 전에 피벗에 대해 좀 더 자세히 알아보자.

피벗(pivot)

  • 퀵 정렬의 실행 시간은 피벗을 선택하는 방법에 따라 달라진다.
  • 이상적으로는 정렬할 데이터 집합의 대략 중앙 값과 거의 일치하도록 피벗을 선택해야 한다.
  • 하지만 중간 값을 알 수 없으니 단순화를 위해 항상 피벗을 첫 번째 요소로 선택한다.

피벗 헬퍼(pivot helper) 함수

  • 퀵 정렬을 구현하려면 먼저 피벗의 양쪽에 배열의 요소 정렬을 담당하는 함수를 구현하는 것이 유용하다.
  • 주어진 배열에서 이 헬퍼 함수는 한 요소를 피벗으로 지정해야 한다.
  • 그런 다음 피벗보다 작은 모든 값이 피벗 왼쪽으로 이동하고, 피벗보다 큰 모든 값이 피벗 오른쪽으로 이동하도록 배열의 요소를 재정렬해야 한다.
  • 피벗 양쪽의 요소 순서는 중요하지 않다. 그낭 기준점보다 큰지 작은지만 구분하여 둔다.
  • 헬퍼 함수는 그 배열에서 이 작업을 해야 한다. 즉, 새 배열을 만들지 않아야 한다.
  • 완료되면 헬퍼 함수가 피벗 인덱스를 반환해야 한다.

피벗 헬퍼 함수 예시

function swapPivot(arr, start = 0, end = arr.length - 1) {
  const pivot = arr[start]; // 좌우로 나누기 위해 비교할 기준 요소 지정
  let swapIdx = start; // pivot의 index

  for (let i = start + 1; i <= end; i++) {
    if (pivot > arr[i]) {
      // pivot보다 작은 요소를 발견할 때
      swapIdx++; // 후에 pivot을 pivot보다 큰 요소 앞에 오게 하기 위해 작은 요소를 발견할 때 마다 ++ 해준다.
      [arr[swapIdx], arr[i]] = [arr[i], arr[swapIdx]]; // 작은 요소를 발견하면 앞으로 땡겨준다.
      console.log(arr);
    }
  }

  [arr[start], arr[swapIdx]] = [arr[swapIdx], arr[start]];
  console.log(arr);

  return swapIdx;
}

swapPivot([4, 6, 9, 1, 2, 5, 3]);

// [4, 1, 9, 6, 2, 5, 3]
// [4, 1, 2, 6, 9, 5, 3]
// [4, 1, 2, 3, 9, 5, 6]
// [3, 1, 2, 4, 9, 5, 6]
// swapIdx: 3
  1. 피벗인 4를 기준으로 작은 값들을 왼쪽으로, 큰 값들을 오른쪽으로 나누어주었다.
  2. 그 다음 피벗이 작은 값들과 큰 값들의 중간으로 갈 수 있도록 계산한 swapIdx 자리로 자리 바꾸기를 해준다.
    (왼쪽으로 간 요소만큼 swapIdx++ 을 해주었기 때문에 나보다 작은 값들 다음에 오는 것이다. 그럼 피벗은 전체 정렬에서 자신의 자리를 찾은 것이다.)
  3. 그리고 swapIdx를 반환해준다.

퀵 정렬 구현

function swapPivot(arr, start, end) {
  const pivot = arr[start]; // 좌우로 나누기 위해 비교할 기준 요소 지정
  let swapIdx = start; // pivot의 index

  for (let i = start + 1; i <= end; i++) {
    if (pivot > arr[i]) {
      // pivot보다 작은 요소를 발견할 때
      swapIdx++; // 후에 pivot을 pivot보다 큰 요소 앞에 오게 하기 위해 작은 요소를 발견할 때 마다 ++ 해준다.
      [arr[swapIdx], arr[i]] = [arr[i], arr[swapIdx]]; // 작은 요소를 발견하면 앞으로 땡겨준다.
      console.log(arr);
    }
  }

  [arr[start], arr[swapIdx]] = [arr[swapIdx], arr[start]];
  console.log(arr);
  console.log("========================");

  return swapIdx;
}

function quickSort(arr, left = 0, right = arr.length - 1) {
  if (left > right) return; // left와 right 지점이 만나면 재귀 종료

  let pivotIdx = swapPivot(arr, left, right); // pivot이 가운데로 옮겨진 index
  // left
  quickSort(arr, left, pivotIdx - 1); // pivot을 기준으로 왼쪽 배열들을 다시 나누어 정렬해준다.
  // right
  quickSort(arr, pivotIdx + 1, right); // pivot을 기준으로 오른쪽 배열들을 다시 나누어 정렬해준다.
}

quickSort([4, 8, 2, 1, 5, 7, 6, 3]);

// [4, 2, 8, 1, 5, 7, 6, 3]
// [4, 2, 1, 8, 5, 7, 6, 3]
// [4, 2, 1, 3, 5, 7, 6, 8]
// [3, 2, 1, 4, 5, 7, 6, 8]
// ========================
// [3, 2, 1, 4, 5, 7, 6, 8]
// [3, 2, 1, 4, 5, 7, 6, 8]
// [1, 2, 3, 4, 5, 7, 6, 8]
// ========================
// [1, 2, 3, 4, 5, 7, 6, 8]
// ========================
// [1, 2, 3, 4, 5, 7, 6, 8]
// ========================
// [1, 2, 3, 4, 5, 7, 6, 8]
// ========================
// [1, 2, 3, 4, 5, 7, 6, 8]
// [1, 2, 3, 4, 5, 6, 7, 8]
// ========================
// [1, 2, 3, 4, 5, 6, 7, 8]
// ========================
// [1, 2, 3, 4, 5, 6, 7, 8]
// ========================

퀵 정렬의 시간복잡도

퀵 정렬은 상황에 따라 시간복잡도가 다르다.

  • 최고의 경우: O(n log n)
    - 합병 정렬과 같다. 전체 배열의 길이가 32인 배열을 합병 정렬한다고 생각해보자.
    그럼 그 배열을 길이가 1 이하인 배열로 나누는데 걸리는 횟수는 4번이다. 즉 log 2인 것이다.
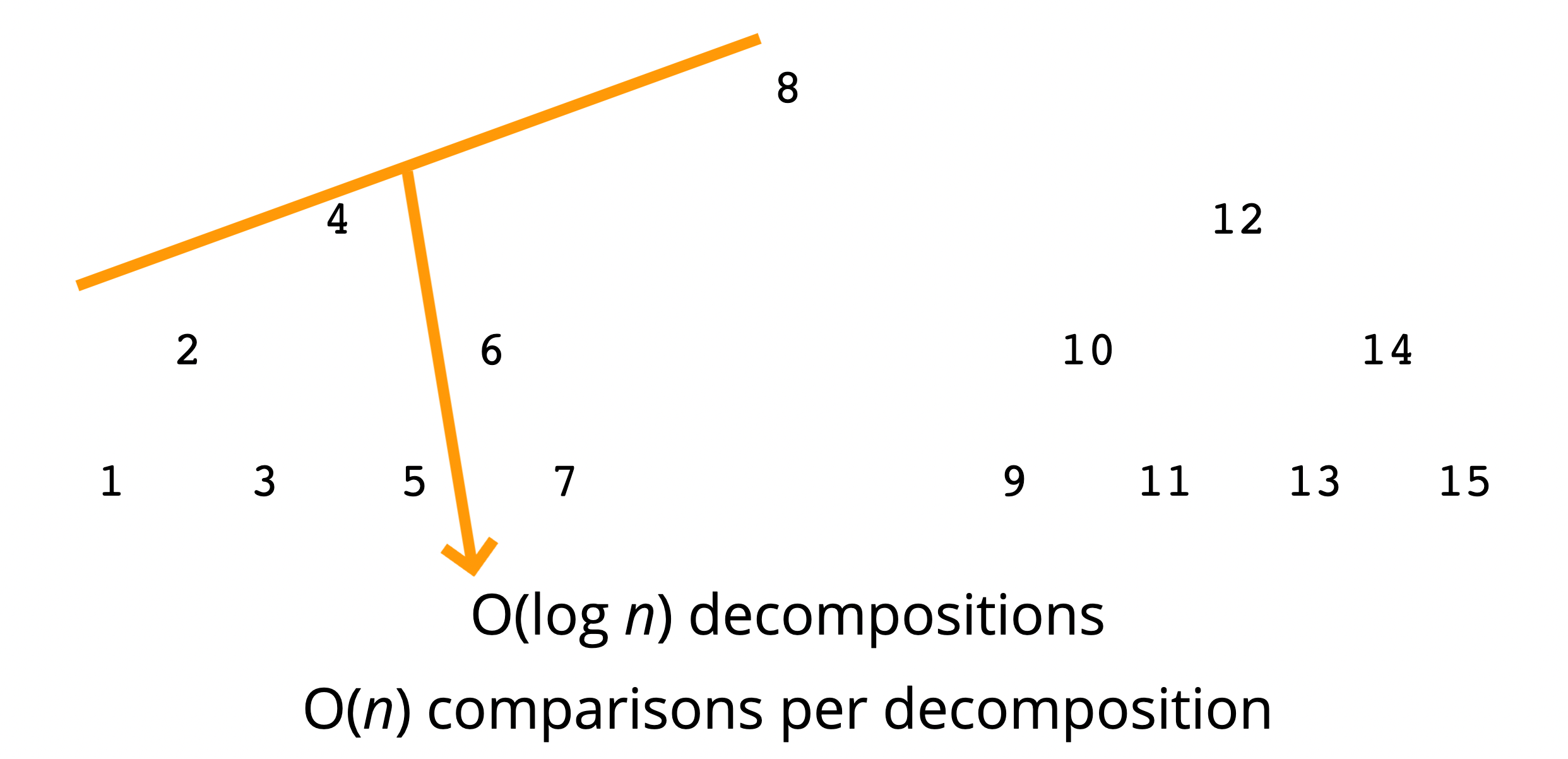
    여기서 나누어준 배열을 swapPivot 함수를 통해 n번씩 비교해주었기 때문에 O(n log n)이 되는 것이다. 퀵 정렬 설명 퀵 정렬 설명

  • 평균: O(n log n)

  • 최악의 경우: O(n2)
    - 선택한 pivot이 항상 최솟값일 경우 퀵 정렬 설명 퀵 정렬 설명 예시의 이미지에서 배열은 이미 정렬이 되어있고 우리가 선택한 pivot은 배열의 첫 번째 요소이다.
    그래서 pivot으로 선택된 값들이 항상 배열에서 제일 작은 수가 된다.
    pivot보다 작은 값들이 없기 때문에 왼쪽으로 가는 값들이 없어 오른쪽의 값들을 계속 나누어준다.
    때문에 n2이 될 수 밖에 없다.
    이런 경우 pivot을 첫 번째 요소가 아닌 가운데의 값을 선택하는 방법을 통해서 최소값이나 최대값을 고르는 것을 피하기 위해 최대한의 노력을 할 수 밖에 없다.

  • 공간복잡도: O(log n)

참고