Dony :)

FE로 성장 중 🌱

삽입 정렬이란?

삽입 정렬은 버블 정렬이나 선택 정렬과 꽤 비슷하다.
그렇지만 몇 가지 중요한 차이점도 있는데, 앞의 정렬들과 달리 삽입 정렬은 실제로 유용한 상황이 있다.
그것은 후에 예시를 통해 알아보도록 하자.

  • 손안의 카드를 정렬하는 방법과 유사하다.
    - 새로운 카드를 기존의 정렬된 카드 사이의 올바른 자리를 찾아 삽입한다.
    - 새로 삽입될 카드의 수만큼 반복하게 되면 전체 카드가 정렬된다.
  • 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다.
  • 매 순서마다 해당 원소를 삽입할 수 있는 위치를 찾아 해당 위치에 넣는다.

정렬 방법

  1. 배열에서 두 번째 요소를 시작 요소로 지정한 뒤, 그 앞(왼쪽)의 요소들과 비교하여 삽입할 위치를 찾은 뒤, 해당 위치로 요소의 자리를 바꾸어준다.
  2. 그 다음은 세 번째 요소를 시작 요소롤 지정한 뒤, 그 앞의 요소들과 똑같이 비교하여 삽입한다.
    - 이렇게 되면 두 번째 요소는 첫 번째 요소만, 세 번째 요소는 두 번째, 첫 번째 요소와 … 회전 후 선택된 요소들의 앞의 요소들과 비교하면서 자리를 바꾸어준다.
  3. 배열이 정렬될 때까지 반복한다.

정렬 알고리즘 예시 시각화 사이트: https://visualgo.net/en/sorting

< 예시 >

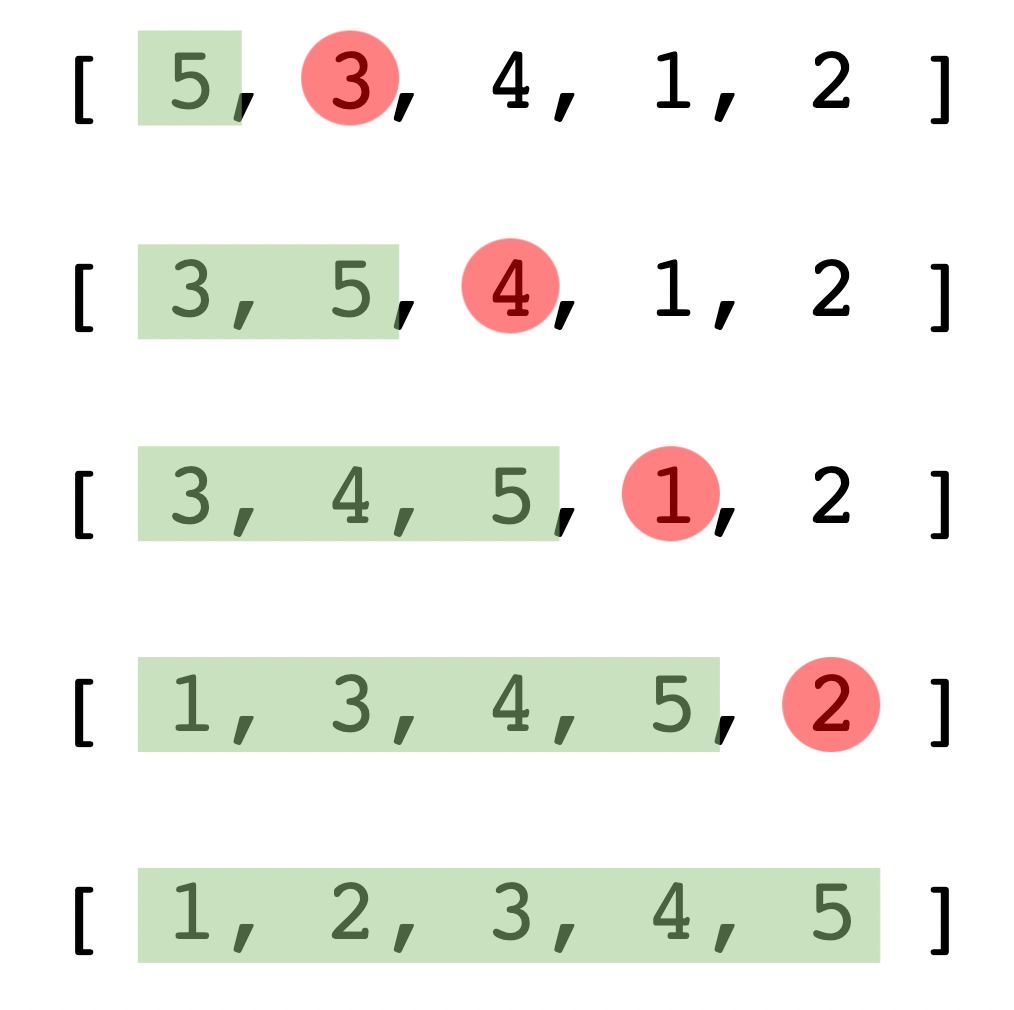삽입 정렬 설명 이미지 위의 예시 이미지를 보면
1-1. 두 번째 요소인 3을 5와 비교해 앞으로 자리 이동한다.

2-1. 세 번째 요소인 4를 5와 비교해 앞으로 자리 이동한다.
2-2. 세 번째 요소인 4와 3을 비교해 3보다 크므로 자리 이동하지 않는다.

3-1. 네 번째 요소인 1을 5와 비교해 앞으로 자리 이동한다.
3-2. 네 번째 요소인 1을 4와 비교해 앞으로 자리 이동한다.
3-3. 네 번째 요소인 1을 3와 비교해 앞으로 자리 이동한다.

4-1. 다섯 번째 요소인 2를 5와 비교해 앞으로 자리 이동한다.
4-2. 다섯 번째 요소인 2를 4와 비교해 앞으로 자리 이동한다.
4-3. 다섯 번째 요소인 2를 3와 비교해 앞으로 자리 이동한다.
4-3. 다섯 번째 요소인 2를 1와 1보다 크므로 자리 이동하지 않는다.

삽입 정렬 구현

그럼 이제 삽입 정렬을 구현해보자.

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    const currentVal = arr[i]; // 비교 기준 요소을 저장
    let j = i - 1;
    while (j >= 0 && arr[j] > currentVal) {
      // j가 음수값으로 가면 안되므로, j >= 0
      // arr[j](arr[i-1]) <= arr[i] 이면 이미 앞부분이 정렬되있는 것이므로 arr[j] > arr[i]일때만 loop를 돌도록 한다.
      console.log(arr[j], arr[i]);
      arr[i] = arr[j];
      // arr[j] > currentVal 이므로 arr[i](currentVal)자리에 바꾸어 주려는 지점의 요소를 대입한다.
      j--;
    }
    arr[j + 1] = currentVal; // j가 다 순회한 뒤 그 지점에 저장해둔 currentVal를 대입한다.
    console.log(arr);
  }

  return arr;
}

insertionSort([2, 1, 76, 9, 31, 16, 4]);

// 2 1
// [1, 2, 76, 9, 31, 16, 4]
// [1, 2, 76, 9, 31, 16, 4]
// 76 9
// [1, 2, 9, 76, 31, 16, 4]
// 76 31
// [1, 2, 9, 31, 76, 16, 4]
// 76 16
// 31 76
// [1, 2, 9, 16, 76, 31, 4]
// 31 4
// 76 31
// 16 76
// 9 16
// [1, 2, 4, 16, 76, 31, 9]

삽입 정렬의 시간복잡도

삽입 정렬은 경우에 따라 시간복잡도가 다르다.

(오름차순 기준)

  • 최악의 경우: O(n2)
    - 정렬하려는 기준의 완전 반대 경우
    ex) [4, 3, 2, 1]
  • 평균: O(n2)
  • 최고의 경우: O(n)
    - 거의 정렬되어 있지만 일부만 되있지 않을 경우
    ex) [1, 2, 3, 0] - 이미 정렬되있는 데이터에 실시간으로 데이터가 계속해서 들어오는 중에 정렬해야할 경우
    (삽입 정렬은 배열의 한 쪽에 정렬된 부분을 두고 한 번에 하나씩 요소들을 삽입하는 방식이기 때문이다.
    어떤 숫자가 입력되든지 상관없이 그 숫자가 가야할 곳으로 보낼 수 있으므로!)
  • 공간복잡도: O(1)

참고