버블 정렬(Bubble sort)

2021.12.13

버블 정렬이란?

미리 말하자면 버블 정렬은 잘 쓰이지 않는다. 느려고 효율적이지 않기 때문이다.
그러나 버블 정렬을 알면 다른 알고리즘들이 왜 효율적인지를 이해하기 수월할 것이다.
그러니 넘어가지 말고 버블 정렬이 왜 비효율적인지 알아보도록 하자!
(오름차순 기준)

순회하면서 큰 값이 맨 뒤로 가는 형태라 계속 반복하여 부풀어 오른다하여 버블 정렬이라 한다.
해당 요소와 뒤의 요소를 하나씩 비교해가며 큰 값이 뒤로 가도록 바꾸어주고, 다 회전한 다음 다시 처음부터 회전을 반복하여 전체 요소가 정렬 순서에 맞을 때까지 반복하는 방식이다.

정렬하기 전, swap 하기

우선 정렬을 하기 전에 swap 기능(자리 바꾸기)을 먼저 이해해야 한다.
많은 정렬 알고리즘은 특정 유형의 스와핑 기능(예를 들어 숫자로 스와핑하여 순서대로 배열)을 포함한다.
아래의 두가지 방법을 보자.

// ES5
function swap(arr, idx1, idx2) {
  var temp = arr[idx1];
  arr[idx1] = arr[idx2];
  arr[idx2] = temp;
}

첫 번째 방법은 전체 배열과 바꾸어주려는 두 인덱스를 매개 변수로 받는다.
그 다음 첫 번째 인덱스의 요소를 temp에 저장한 뒤, 첫 번째 요소에 두번 째 요소를 대입한다.
마지막으로 두번 째 요소에 첫 번째 요소를 저장해 둔 temp를 저장해준다.

// ES2015
const swap = (arr, idx1, idx2) => {
  [arr[idx1], arr[idx2]] = [arr[idx2], arr[idx1]];
};

ES2015로 넘어오면서 구조 분해 할당 기능이 추가 되었다.
해당 기능은 아래의 사이트를 참고하자.
https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Destructuring_assignment#array_destructuring

정렬 방법

현재 index의 요소와 다음 index의 요소를 비교한다.
해당 index의 요소가 더 크다면 자리를 바꾸어주고 아니면 넘어간다.
내부 for문의 index가 증가하면서 현재 index가 다음 index, 다음 index가 다다음 index가 되기 때문에 둘을 비교한다.
해당 index의 요소가 더 크다면 자리를 바꾸어주고 아니면 넘어간다.
모두 정렬될 때까지 반복한다. 정렬 알고리즘 예시 시각화 사이트: https://visualgo.net/en/sorting

< 예시 >

버블 정렬 설명 이미지

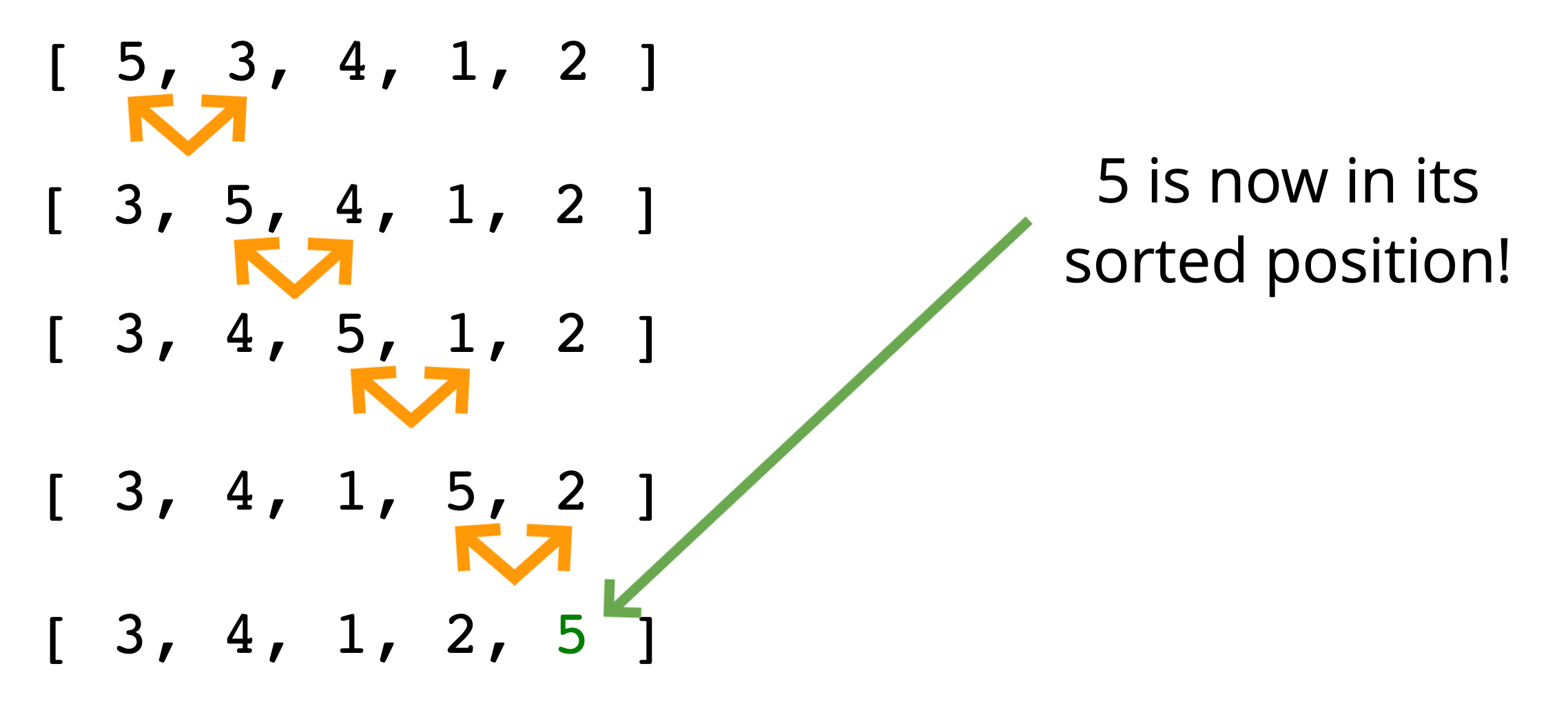
위의 예시 이미지를 보면

5와 3을 비교하여 바꾼다.
5와 4를 비교하여 바꾼다.
5와 1을 비교하여 바꾼다.
5와 2를 비교하여 바꾼다.

5가 이 배열에서 가장 큰 수라서 마지막에 위치해야 하기 때문이다.
이게 한 번 순회하는 과정이다.
그러면 이걸 얼마나 반복해야 할까?
처음에는 배열에 있는 모든 요소에 대해 반복해야 할 수 있다.
하지만 뒤에 요소들을 계속 배치하면서 이 값이 줄어들게 될 것이다. 그 다음 순환에서는 4개, 그 다음은 3개 …
즉, 한번 순회할 때 마다 큰 요소들이 뒤에서 하나씩 쌓이게 되는 것이다.
지금은 제일 큰 5가 제일 뒤에 있고, 그 다음 순회 때는 다음으로 큰 4가 5의 앞에 가고… 이 과정을 반복하는 것이다.
그러면 앞으로 갈 수록 더 적은 요소들만 확인하면 된다.
루프에도 이걸 적용할 수 있다.

버블 정렬 구현

그럼 이제 버블 정렬을 구현해보자.

최적화 하지 않은 구현

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      console.log(arr, arr[j], arr[j + 1]);
      if (arr[j] > arr[j + 1]) {
        // 해당 요소와 다음 요소를 비교하여 자리를 바꾸어 준다.
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }

    console.log("=================================");
  }

  return arr;
}

bubbleSort([37, 29, 8, 45]);

// ES2015
function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      console.log(arr, arr[j], arr[j + 1]);
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }

    console.log("=================================");
  }

  return arr;
}

bubbleSort([37, 29, 8, 45]);

//       arr        arr[j]  arr[j+1]
// [37, 29, 8, 45]    37      29
// [29, 37, 8, 45]    37       8
// [29, 8, 37, 45]    37      45
// [29, 8, 37, 45]    45   undefined
// =================================
// [29, 8, 37, 45]    29       8
// [8, 29, 37, 45]    29      37
// [8, 29, 37, 45]    37      45
// [8, 29, 37, 45]    45   undefined
// =================================
// [8, 29, 37, 45]    8       29
// [8, 29, 37, 45]    29      37
// [8, 29, 37, 45]    37     45
// [8, 29, 37, 45]    45   undefined
// =================================
// [8, 29, 37, 45]    8      29
// [8, 29, 37, 45]    29     37
// [8, 29, 37, 45]    37     45
// [8, 29, 37, 45]    45   undefined

위의 코드를 통해 버블 정렬을 구현할 수 있다.
하지만 보듯이 무조건 배열을 다 돌아야하기 때문에 이미 정렬되어 있는 요소들도 순회하게 된다.
또한 맨끝의 요소는 그 다음 요소가 없기 때문에 undefined와 비교하게 되어 불필요한 순회 횟수가 많아지는 것이다.

최적화 1: 반복문 범위 좁히기

function bubbleSort(arr) {
  for (let i = arr.length; i > 0; i--) {
    // 순회할 때마다 끝은 큰 숫자가 가게 되므로 끝에서부터 하나씩 줄어든 범위로 순회
    for (let j = 0; j < i - 1; j++) {
      // i - 1까지 돌아 undefined와 비교하지 않도록
      console.log(arr, arr[j], arr[j + 1]);

      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }

    console.log("=================================");
  }

  return arr;
}

//       arr        arr[j]  arr[j+1]
// [37, 29, 8, 45]    37      29
// [29, 37, 8, 45]    37      8
// [29, 8, 37, 45]    37      45
// =================================
// [29, 8, 37, 45]    29      8
// [8, 29, 37, 45]    29      37
// =================================
// [8, 29, 37, 45]    8       29
// =================================
// =================================

앞선 코드의 문제점을 개선한 코드이다.
하지만 해당 코드 또한 지난 순회에서 자리 바꾸기를 한 부분을 다시 탐색하고 있다. 이미 정렬이 끝난 상황에서도 끝까지 순회을 하는 것이다.

최적화 2: 이미 정렬한 부분인지 확인

그럼 앞의 문제점을 다시 개선하기 위해 우리는 확인을 해야한다.
지난 번 순회에서 자리 바꾸기를 했는지 말이다.

function bubbleSort(arr) {
  let noSwaps; // swap한 적이 있는지 체크해 줄 변수 생성

  for (let i = arr.length; i > 0; i--) {
    noSwaps = true; // 외부 함수를 순회할 때마다 swap를 true로 초기화 (매번 swap가 없다고 가정)

    for (let j = 0; j < i - 1; j++) {
      console.log(arr, arr[j], arr[j + 1]);
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
        noSwaps = false; // 지난 순회에서 swap를 했으면 false로 변경
      }
    }

    console.log("=================================");
    console.log(noSwaps);
    if (noSwaps) break; // true인 경우(지난 순회에서 swap를 하지 않았다. => 더 이상 swap하지 않아도 된다.) break!
  }

  return arr;
}

bubbleSort([37, 29, 8, 45]);

//       arr        arr[j]  arr[j+1]
// [37, 29, 8, 45]    37       29
// [29, 37, 8, 45]    37       8
// [29, 8, 37, 45]    37       45
// =================================
// false
// [29, 8, 37, 45]    29       8
// [8, 29, 37, 45]    29       37
// =================================
// true
// [8, 29, 37, 45]    8        29
// =================================

버블 정렬의 시간복잡도

반복문 순회 수를 얼마나 줄이느냐에 따라 Big O가 달라지니 잘 생각할 것!

최악의 경우: O(n²)
- 최적화를 하지 않은 코드
평균: O(n²)
최고의 경우: O(n) - 최적화를 통해서 총 루프횟수는 n번만큼 순회 후, 다시 한번 돌면서 이전에 swap이 되지 않았다는 것을 확인하고, break를 해주었으므로 O(2N), 즉 O(N)이다.
공간복잡도: O(1)

Dony :)