이진 트리(Binary Tree)와 이진 탐색 트리(Binary Search Tree)

2021.12.20

이진 트리란?

이진 트리는 트리 구조 중에서 각 노드가 최대 2개의(0~2개) 자식을 가지는 트리 구조이다.
< 옳은 예시 >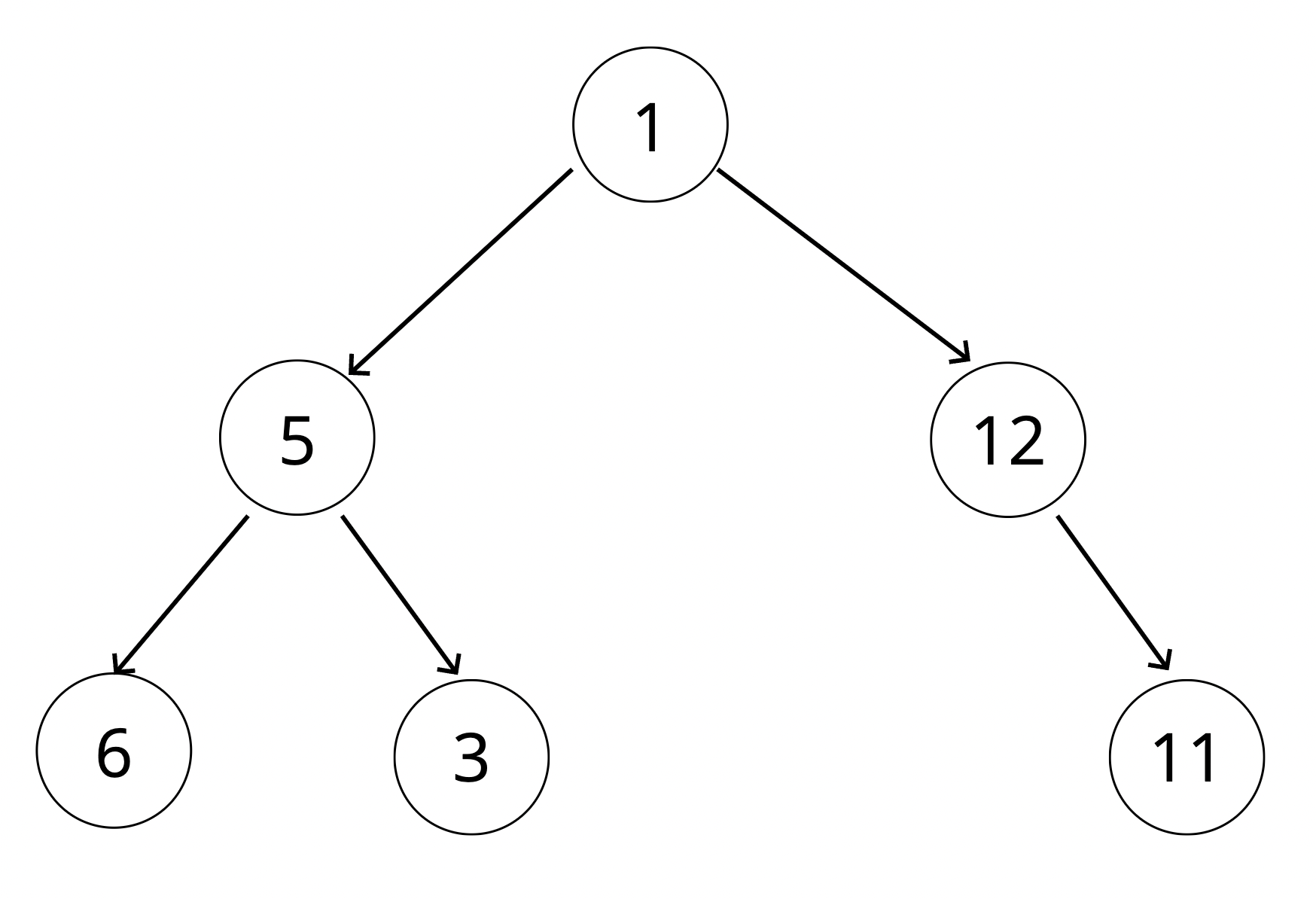 < 틀린 예시 > 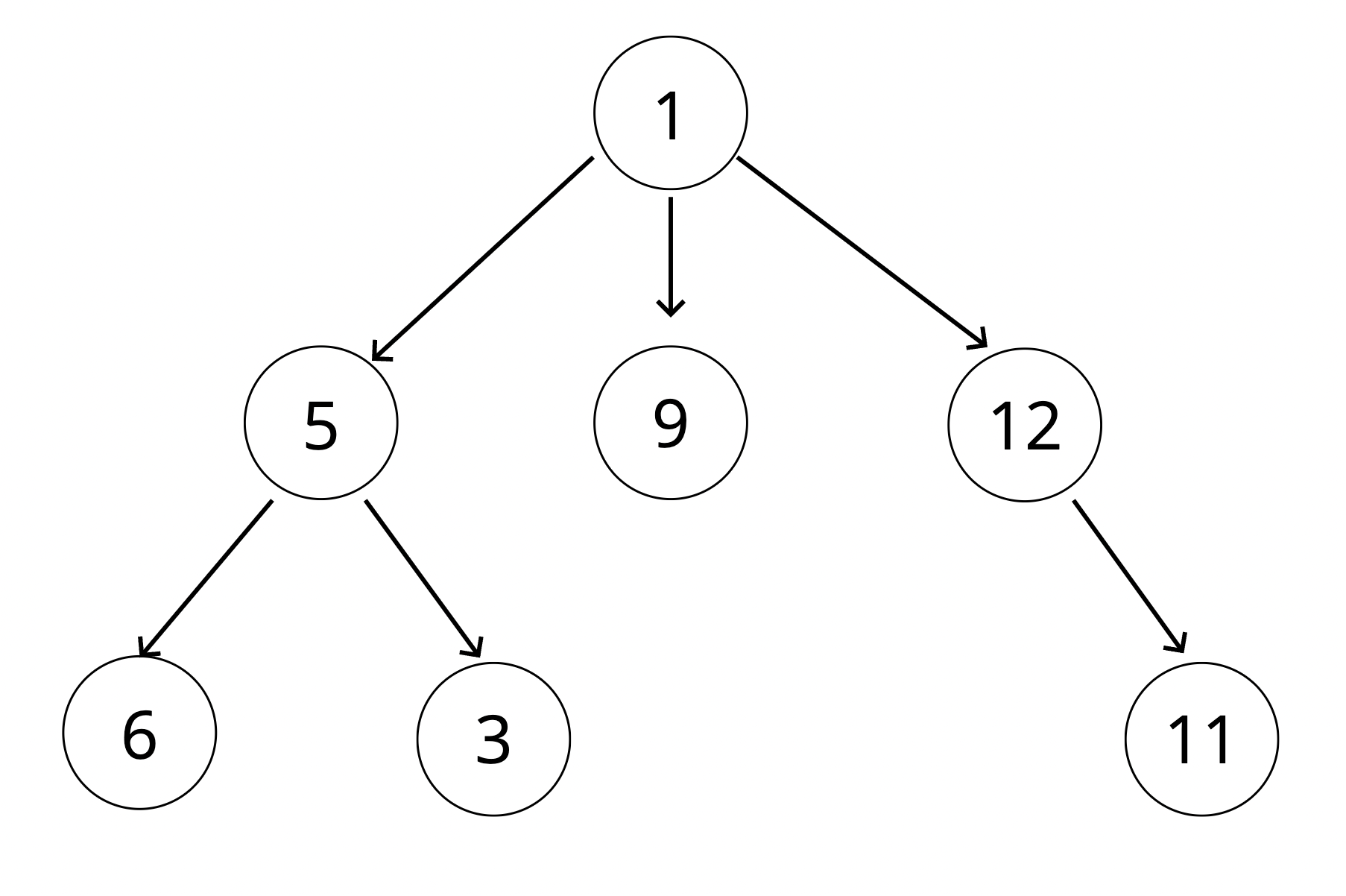3개의 자식을 가지므로 이진 트리가 아닌 그냥 트리 구조
순회가 쉽다는 장점이 있다.

이진 탐색 트리란?

이진 트리에 속해 있는 이진 트리의 특별한 종류이다.
이진 트리와 달리 퀵 소트처럼 작은 수가 왼쪽, 큰 수가 오른쪽으로 정렬되어 있다.
< 옳은 예시 >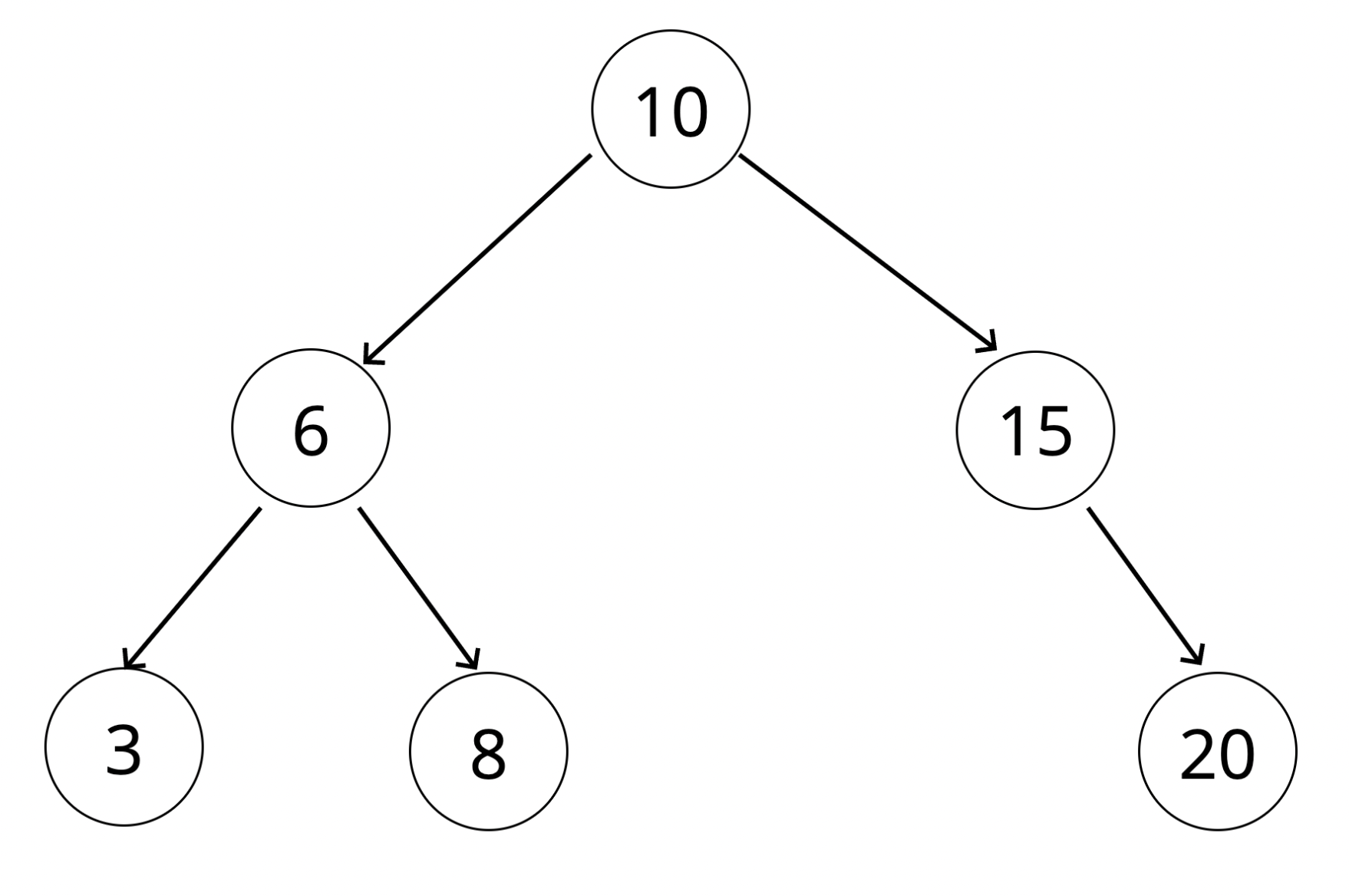 < 틀린 예시 > 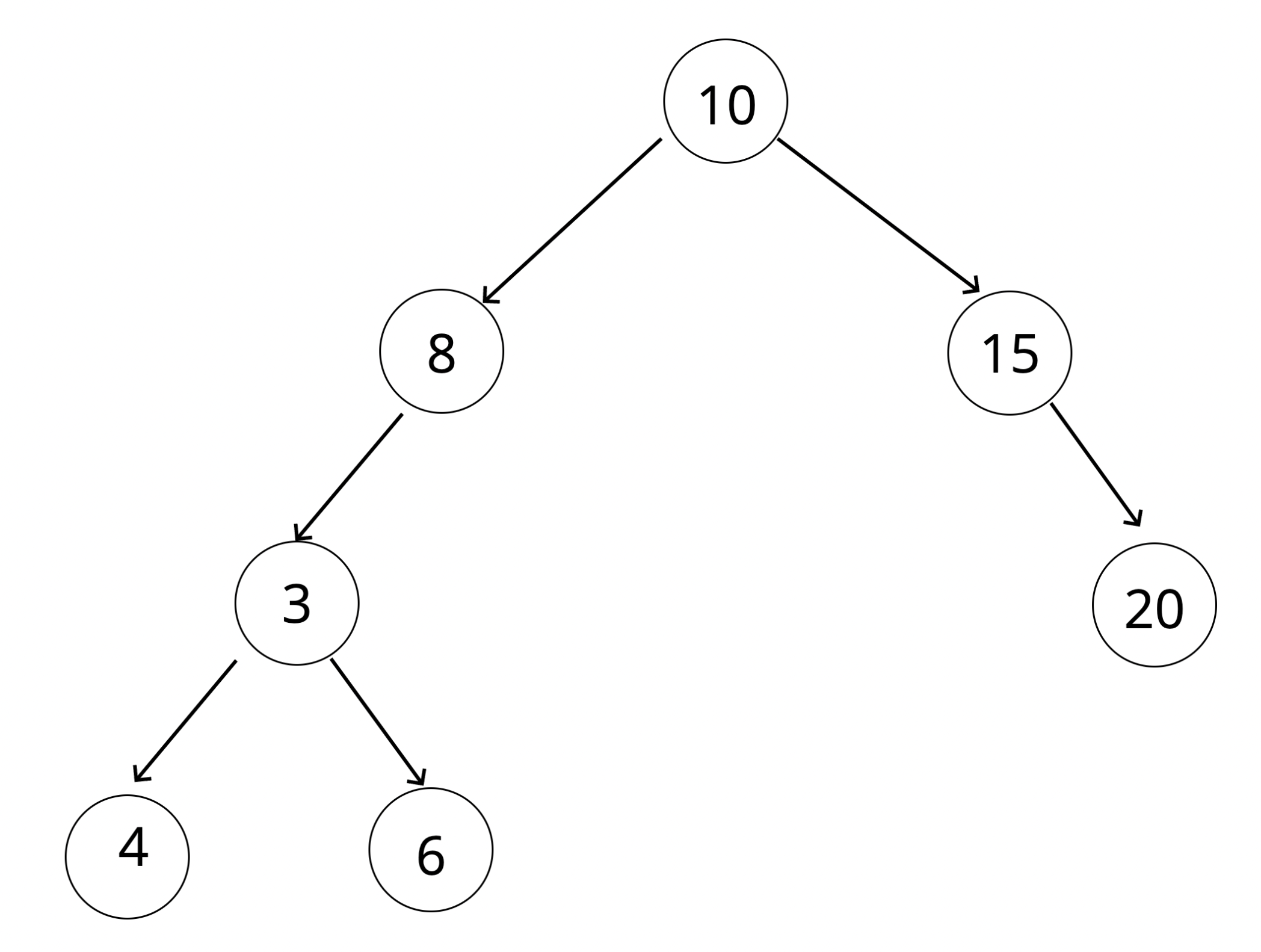맨 아래의 4는 3보다 크므로 이진 탐색트리가 아닌 이진 트리이다.
이진 탐색(binary search)과 연결 리스트(linked list)를 결합한 자료구조의 일종이다.
이진 탐색으로 정렬되어 있기 때문에 효율적인 탐색 능력을 유지하면서도, 빈번한 자료 입력과 삭제를 가능하게끔 고안됐다.

이진 탐색 트리 구현

이중 연결 리스트와 비슷한 방식이다.

이중 연결 리스트	이진 탐색 트리
prev	left
next	right
head	root

insert

정렬 기준에 맞는 위치에 노드를 추가해주는 메서드

추가할 새로운 노드를 만든다.
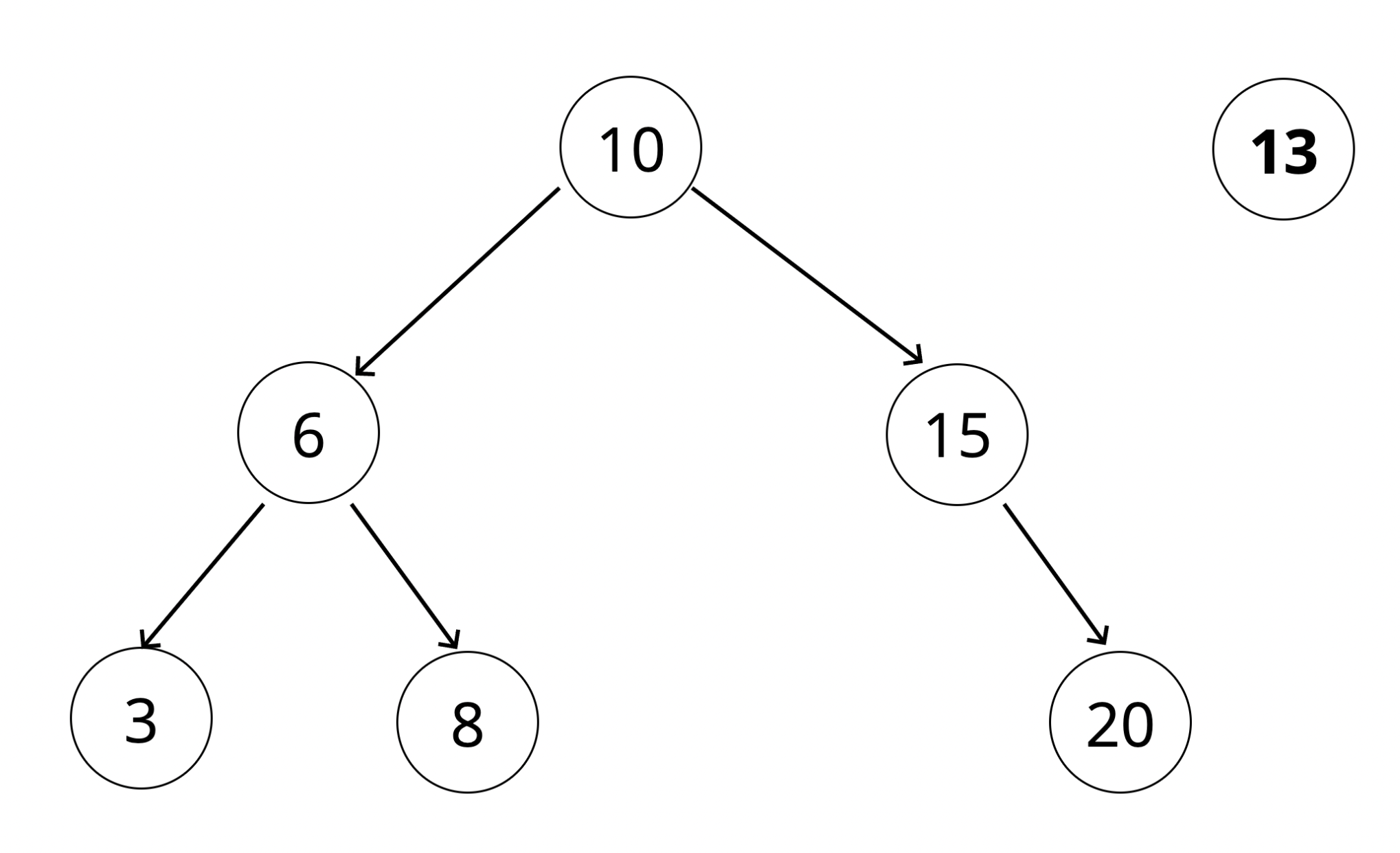
루트에서 출발한다.
루트가 있는지 확인한다.
루트가 없는 경우, 새 노드가 루트가 된다.
루트가 있는 경우,

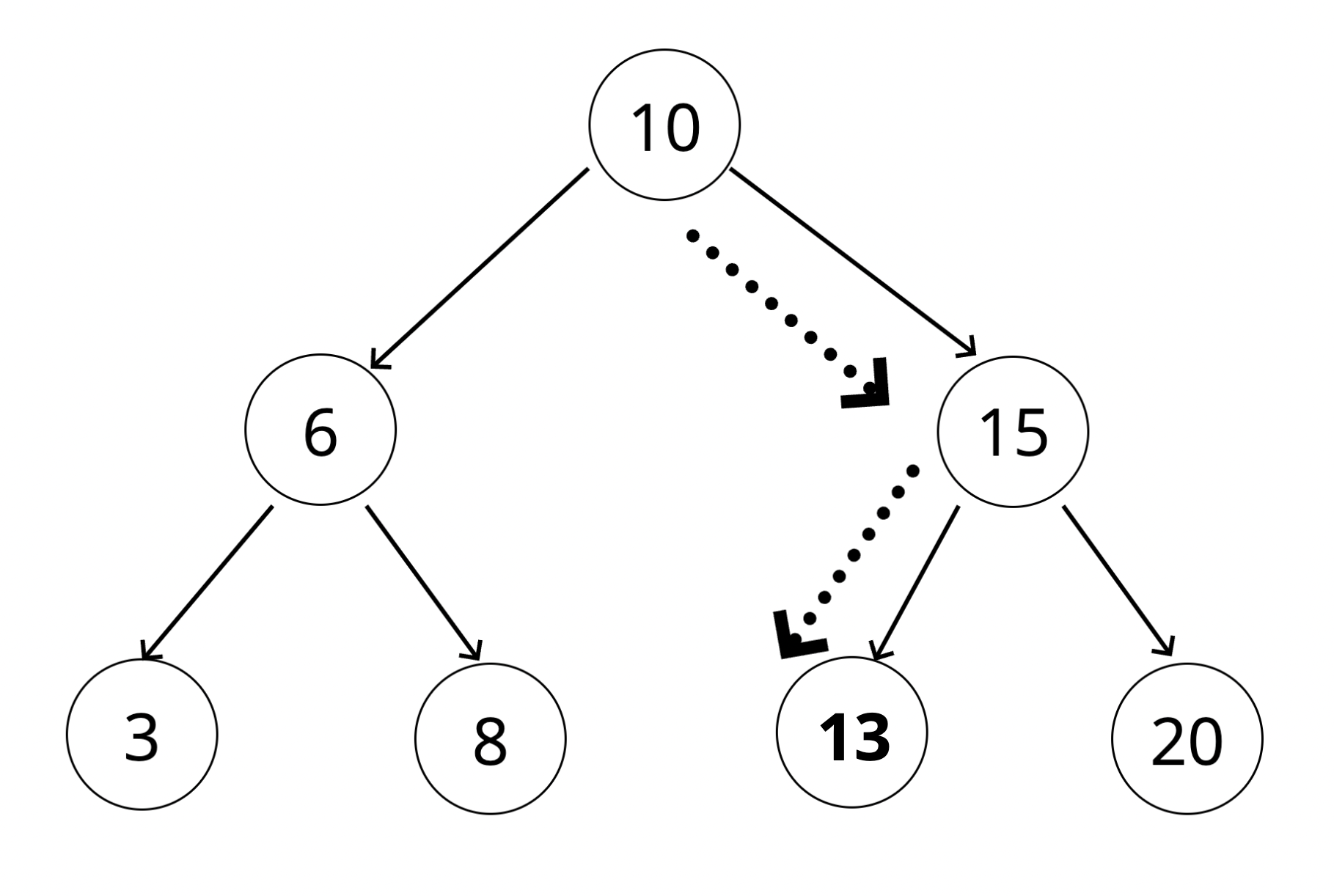
새 노드의 값이 루트의 값보다 큰지 작은지 확인한다.
크면 오른쪽에, 작으면 왼쪽에 노드가 있는지 확인한다.
있는 경우 해당 노드로 이동하고 이 단계를 반복한다.
없는 경우 해당 노드를 왼쪽 속성으로 추가한다.

추가한 노드를 반환한다.

class Node {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  insert(value) {
    const newNode = new Node(value);
    if (this.root === null) {
      // 빈 트리일 때
      this.root = newNode; // root를 새로 추가할 노드로 설정
      return this; // 추가한 노드를 반환
    }
    let current = this.root; // 순회할 때 현재 노드, root부터 탐색 시작하기 위해 초기값으로 설정
    while (true) {
      // 새로운 노드가 들어갈 위치를 찾고, 그 값을 반환할 때까지 순회
      if (value === current.value) return undefined; // 추가하려는 값이 기존에 있다면
      if (value < current.value) {
        // 추가할 값이 현재 노드보다 작으면
        if (current.left === null) {
          // 현재 노드의 왼쪽이 비어있으면
          current.left = newNode; // 왼쪽을 새로운 노드로 지정
          return this; // 추가한 노드를 반환
        }
        current = current.left; // 비어있지 않으면 왼쪽 자식으로 더 내려간다.
      } else {
        // 추가할 값이 현재 노드보다 크면
        if (current.right === null) {
          // 현재 노드의 오른쪽이 비어있으면
          current.right = newNode; // 오른쪽을 새로운 노드로 지정
          return this; // 추가한 노드를 반환
        }
        current = current.right; // 비어있지 않으면 오른쪽 자식으로 더 내려간다.
      }
    }
  }
}

const tree = new BinarySearchTree();
tree.insert(30);

find

찾고자 하는 노드를 찾아주는 메서드

루트에서 출발한다.
루트가 있는지 확인한다.
루트가 없는 경우, false를 반환한다.
루트가 있는 경우,

해당 노드의 값이 찾는 값인 경우, 해당 노드를 반환한다.
찾는 값이 아닌 경우, 값이 루트 값보다 큰지 작은지 확인한다.
크면 오른쪽에, 작으면 왼쪽에 노드가 있는지 확인한다.
있는 경우 해당 노드로 이동하고 이 단계를 반복한다.
없는 경우 undefined를 반환한다.

찾은 노드를 반환한다.

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  find(value) {
    if (this.root === null) return false; // 빈 트리일 때
    var current = this.root; // 순회할 때 현재 노드, root부터 탐색 시작하기 위해 초기값으로 설정
    while (current) {
      // 더 이상 내려갈 노드가 없을 때까지 순회
      if (value === current.value) return current; // 찾는 값이 현재 노드의 값과 같으면
      if (value < current.value) {
        // 찾는 값이 현재 노드의 값보다 작으면
        current = current.left; // 왼쪽 자식으로 더 내려간다.
      } else if (value > current.value) {
        // 찾는 값이 현재 노드의 값보다 크면
        current = current.right; // 오른쪽 자식으로 더 내려간다.
      }
    }
    return undefined; // 값이 없음을 반환
  }
}

const tree = new BinarySearchTree();
tree.find(30);

contains

확인하고자 노드가 있는지 여부를 확인해주는 메서드

루트에서 출발한다.
루트가 있는지 확인한다.
루트가 없는 경우, false를 반환한다.
루트가 있는 경우,

해당 노드의 값이 확인할 값인 경우, true를 반환한다.
확인할 값이 아닌 경우, 값이 루트 값보다 큰지 작은지 확인한다.
크면 오른쪽에, 작으면 왼쪽에 노드가 있는지 확인한다.
있는 경우 해당 노드로 이동하고 이 단계를 반복한다.
없는 경우 false를 반환한다.

true를 반환한다.

class BinarySearchTree {
  constructor() {
    this.root = null;
  }
  contains(value) {
    if (this.root === null) return false; // 빈 트리일 때
    var current = this.root; // 순회할 때 현재 노드, root부터 탐색 시작하기 위해 초기값으로 설정
    while (current) {
      // 더 이상 내려갈 노드가 없을 때까지 순회
      if (value === current.value) return true; // 찾는 값이 현재 노드의 값과 같으면
      if (value < current.value) {
        // 찾는 값이 현재 노드의 값보다 작으면
        current = current.left; // 왼쪽 자식으로 더 내려간다.
      } else if (value > current.value) {
        // 찾는 값이 현재 노드의 값보다 크면
        current = current.right; // 오른쪽 자식으로 더 내려간다.
      }
    }
    return false; // 포함되어 있지 않음을 반환
  }
}

const tree = new BinarySearchTree();
tree.contains(30);

이진 탐색 트리의 Big O

삽입
- O(log n)
- insert
- 노드의 크기에 따라 이중으로 나눠져있기 때문에 모든 원소를 탐색하지 않는다.
- 최악의 경우가 트리의 높이 만큼 탐색하는 경우이다.
  때문에 depth를 H라고 했을 때 시간복잡도를 O(H) 라고도 할 수 있다.

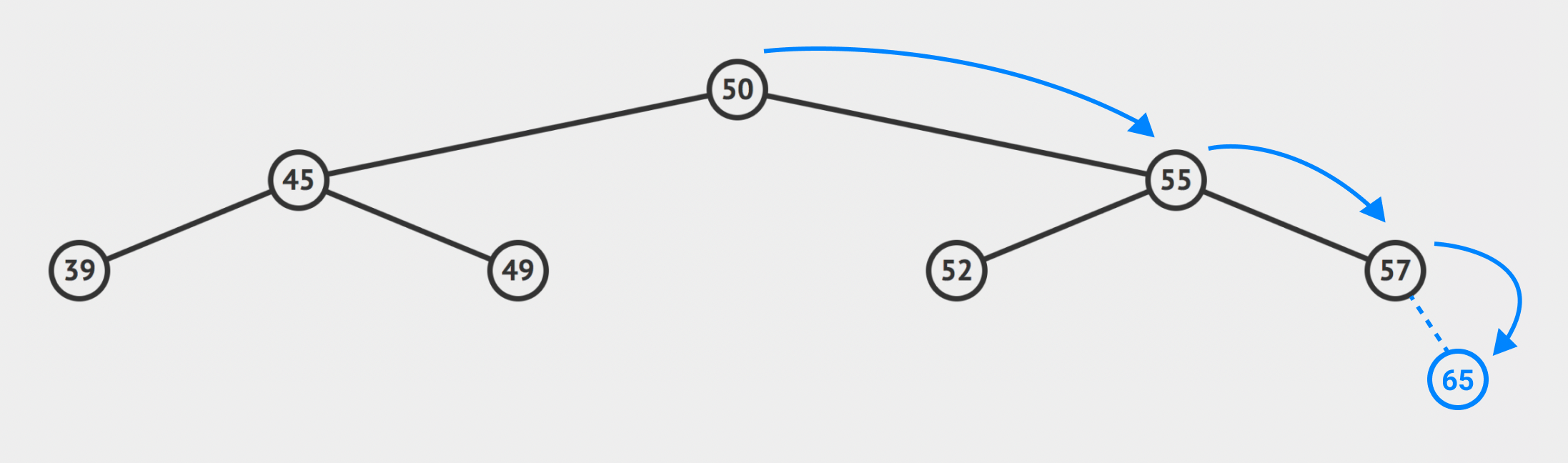위의 이진 탐색 트리에서 65를 추가한다고 했을 때 오른쪽으로 3depth 만큼 내려가야 한다. 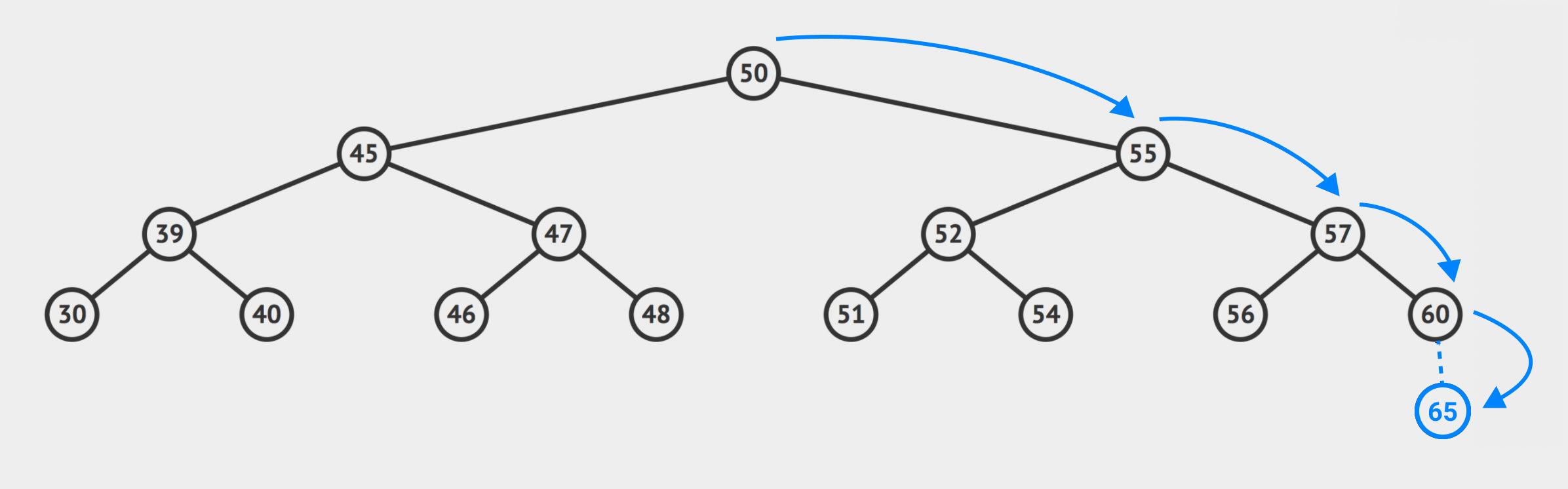여기서 노드의 갯수가 두배로 늘어나 1depth가 추가됐을 경우 65는 4depth 만큼 내려가야 한다. 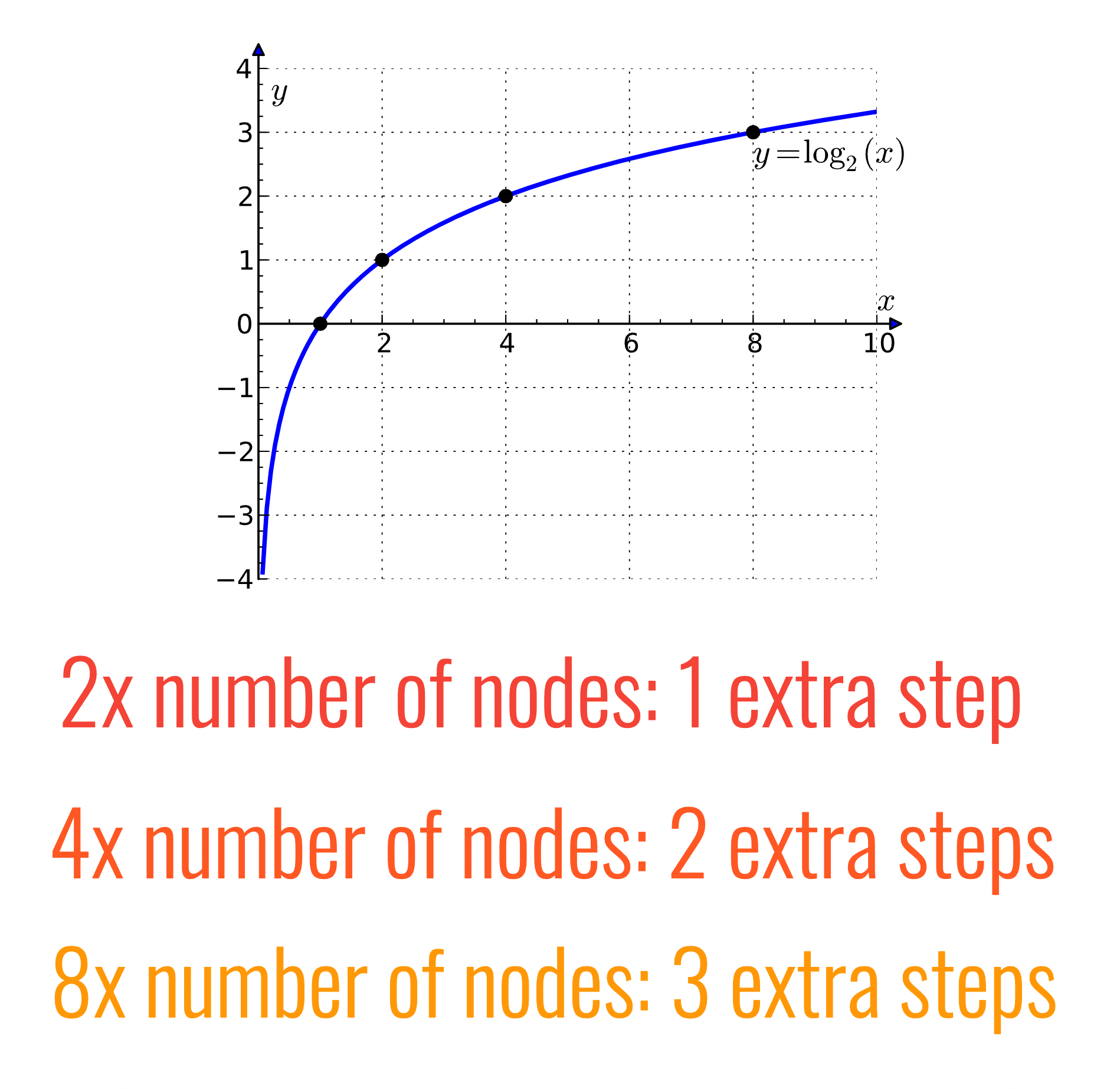즉, 노드가 2배로 늘어날수록 가야하는 depth의 길이가 늘어가게 된다.
때문에 삽입의 시간복잡도는 O(H)이고, O(H)는 O(log N)과 같다.

탐색
- O(log n)
- find, contains
- 삽입과 같이 최악의 경우 트리의 높이 만큼 탐색해야하므로 시간복잡도는 O(log n)이다.

Dony :)