Dony :)

FE로 성장 중 🌱

Big O 표기법은 무엇이며 필요한 이유는?

한 문제에 두가지 해결 방법이 있다고 했을 때, 어느 것이 더 좋을까?
Big O 표기법은 이런 질문에 관한 것이다.
코드를 일반화하고 코드에 대해 말해주고 코드의 상대적 성과를 비교하는 방법을 말한다.
지진 강도를 나타낼 때, 강한 지진이란 표현이 아니라 7.2지진, 9.4지진 등과 같이 표현하는 것처럼 Big O 표기법도 코드의 일반화를 통해 애매한 측량을 정형화한 방법이다.
알고리즘에 입력값이 커짐에 따라 실행 시간이 늘어나는 정도를 정리해서 알려주는 것이다.
Big O 표기법은 아주 큰 그림, 높은 수준에서 추세를 관찰해서 입력값의 크기가 커짐에 따라서 실행시간이나 공간 복잡도가 어떻게 변하는지를 보여준다.
빅오로 측정한 시간 복잡도와 공간 복잡도는 알고리즘 그 자체에 따라 다른 것으로, 하드웨어와는 무관핟.

코드에서 더 나은 기준은?

  • 속도는 빠른가?
  • 메모리를 얼마나 사용하는가?
  • 가독성이 좋은가?

속도와 메모리가 더 중요하지만 아쉽게도 위의 두가지는 가독성을 해치는 경우가 많다.
그렇지만 큰 데이터를 다룰 때는 위의 두가지를 우선으로 해야한다.
당연한 말이지만 좋은 코드란 세가지의 균형이 잘 잡힌 것.
메모리를 너무 많이 잡아먹지 않으면서 읽기 좋은 코드를 작성해야한다.
필자의 생각이지만 알고리즘 측면에서는 속도가 최우선이지만 유지보수를 해야하는 상황이라면 메모리와 가독성도 중요할 것이다.

시간 복잡도

코드를 실행하는데 걸리는 시간을 시간 복잡도라고 한다.

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

function addUpTo(n) {
  return n * (n + 1) / 2;
}

위와 같이 한 문제에 두 가지 풀이법이 있을 때, 이 두 가지 풀이의 속도를 어떻게 알 수 았을까?

내장 시간 측정 함수 활용

performance.now() 를 사용하여 브라우저에서 문서가 만들어지는 순간 시간과
addUpTp 함수를 실행한 뒤 시간을 측정하여 둘의 차이를 구하는 것이다.

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)
// Time ElapsedL 1.257500000006985 seconds.

function addUpTo(n) {
  return n * (n + 1) / 2;
}

let t1 = performance.now();
addUpTo(1000000000);
let t2 = performance.now();
console.log(`Time Elapsed: ${(t2 - t1) / 1000} seconds.`)
// Time ElapsedL 0.00010000000474974513 seconds.

위의 방법으로 봤을 때, 두번 째 코드의 속도가 더 빠른 것을 알 수 있다.
그렇지만 이 방법이 가장 정확한 시간 측정 방법은 아니다.
한 컴퓨터에서 한 코드로 반복 실행해도 시간이 다르게 측정되기도 한다.
이 말은 각각 다른 컴퓨터에서 한 코드를 실행하면 시간이 다르게 측정되기도 한다는 것이다.
컴퓨터의 성능이나 환경에 따라 각각 다르게 출력되기도 하고,
특히 알고리즘은 속도가 빠르기 때문에 근사한 차이를 정확히 측정할 수 없을 경우도 있기 때문이다.

컴퓨터가 동작해야하는 횟수 세기

컴퓨터의 성능에 따라 시간은 달라질 수 있지만, 코드의 실행 횟수에 따라 시간은 결정되므로
코드에서 실행되는 횟수를 세어보는 방법이다.

function addUpTo(n) {
  return n * (n + 1) / 2;
}

위의 코드를 보면 곱하기, 더하기, 나누기 총 3개의 단순 동작이 일어난다.

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

그러나 위의 코드를 보면

  1. let total = 0 에서 할당 1번
  2. let i = 0 에서 할당 1번
  3. i <= n 에서 비교 1번
  4. i++ 에서 더하기, 할당으로 2번
  5. total += i 에서 더하기, 할당으로 2번

보여지는 소스에서만 7번의 동작이 일어난다.
그러나 n이 10이라고 한다면 for문에서의 동작 3, 4, 5번은 10번 실행되게 되고,
그럼 총 52번의 실행이 일어나게 된다.
위의 코드와 달리 n이 커질수록 속도가 더 오래걸리게 되는 것이다.
결국 이런 동장 과정은 n에 비례하기 때문에 일일히 세기가 힘들다.
때문에 Big O 와 같은 도식화한 표기법이 필요한 것이다.

Big O 표기법

n이 증가함에 따라 컴퓨터가 해야 하는 간단한 연산의 수가 결국 상수 곱하기 f(n)보다 작으면 알고리즘은 O(f(n)라고 한다.

  • f(n)는 상수일 수 있다. (f(n) = 1) => O(1)
  • f(n)는 선형일 수 있다. (f(n) = n) => O(n)
  • f(n)는 (f(n) = n)2일 수 있다. => O(n2)
  • f(n)는 완전히 다른 것일 수 있다.

O(1)

function addUpTo(n) {
  return n * (n + 1) / 2;
}

위의 코드를 Big O 표기법으로 다시 본다면 O(1)이다.
앞에서도 봤듯이 n의 값이 무엇이든 1번만 실행되기 때문이다.
여기서 n의 값이 얼마인지는 중요하지 않다.
n의 값이 얼마이든지 실행 횟수는 같기 때문이다.
때문에 Big O 표기법에서 상수는 중요하지 않다.

O(n)

function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

위의 코드는 Big O 표기법으로 했을 때 O(n)이다. 정확히는 O(5n+2) 이다.
그러나 앞에서 말했듯이 Big O 에서 상수는 중요하지 않다.
5n이던 n이던 n+2이던 n의 값에 따라 일정하게 증가하기 때문에 전체적인 그래프가 일직선인 것은 같기 때문이다.

function countUpAndDown(n) {
  console.log("Going up!");
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
  console.log("At the top!\nGoing down...");
  for (let j = n - 1; j >= 0; j--) {
    console.log(j);
  }
  console.log("Back down. Bye!");
}

위의 코드 또한 O(n)+O(n)인 O(2n)이지만 일직선으로 증가하는 것은 같기 때문에 크게 O(n)으로 표기할 수 있다.

O(n2)

function printAllPairs(n) {
  for (var i = 0; i < n; i++) {
    for (var j = 0; j < n; j++) {
      console.log(i, j);
    }
  }
}

이중 for문일 경우 O(n) 안에 O(n)이 있으므로 O(n * n)이다. 즉 O(n2)인 것이다.

Big O 표기법 규칙

  1. 상수는 고려하지 않는다.

  2. 더 작은 단위는 고려하지 않는다.

  3. 산술 연산은 일정하다.
  4. 변수 할당이 일정합니다.
  5. 배열(색인별) 또는 객체(키별)의 요소에 액세스하는 것은 일정합니다.
  6. 루프에서 복잡도는 루프의 길이와 루프 내부에서 일어나는 모든 것의 복잡도를 곱한 것이다.
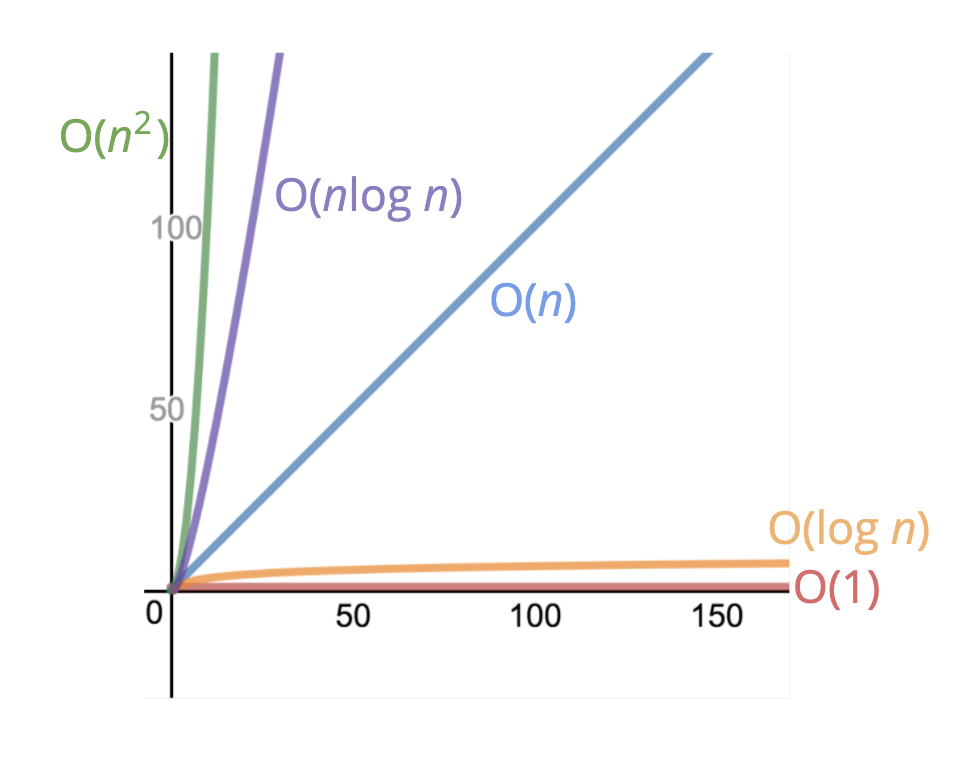    [Big O 표기법 그래프]

https://rithmschool.github.io/function-timer-demo/

공간 복잡도

  • O(1)
    • number, boolean, undefined, null 등 stirng을 제외한 원시값
    • number는 1을 할당하든 1000을 할당하든 차지하는 공간은 같다. 때문에 위의 타입들은 공간복잡도가 O(1)이다.
  • O(n)
    • stirng과 array, object 같은 참조값
    • string은 원시값이지만 문자열의 길이에 따라, array는 배열의 길이에 따라, object는 키의 갯수에 따라 O(n)이 된다.
function sum(arr) {
  let total = 0;
  for (let i = 0; i < arr.length; i++) {
    total += arr[i];
  }
  return total;
}

위의 함수를 보면 total과 i 두가지 number가 있으므로 이 함수의 공간 복잡도만을 봤을 때는 O(2)이다.
즉 O(1)이 되는 것이다.

function double(arr) {
  let newArr = [];
  for (let i = 0; i < arr.length; i++) {
    newArr.push(2 * arr[i]);
  }
  return newArr;
}

다른 함수를 보면 array인 newArr이 있고, for문에 따라 배열의 길이가 늘어나게 되므로, 이 함수의 공간 복잡도는 O(n)이 된다.

시간 복잡도만을 봤을 때는 둘 다 O(n)이지만, 공간 복잡도로 봤을 때는 sum함수가 복잡도가 낫게 되는 것이다.

참고