이진수 (Binary digit, bit)
불 대수 (Boolean Algebra)
- 참 또는 거짓
- 1과 0의 두 가지 상태로 표현하는 논리회로의 간략화를 위해 사용
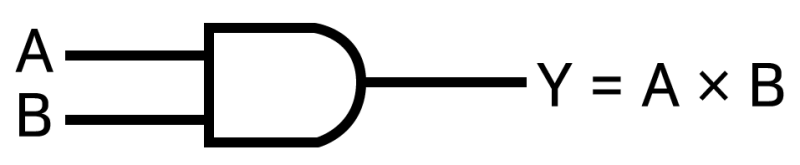
AND 게이트
- A와 B가 모두 1일 때 1
- 두 경우를 곱한 것과 같아서 논리곱이라고 한다.
- A AND B 또는 A・B 또는 AB 로 표시
| A |
B |
AND |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
OR 게이트
- A와 B 둘 중 하나 이상 1일 때 1
- 두 경우를 더한 것과 같아서 논리합이라고 한다.
- A OR B 또는 A+B 로 표시

| A |
B |
OR |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
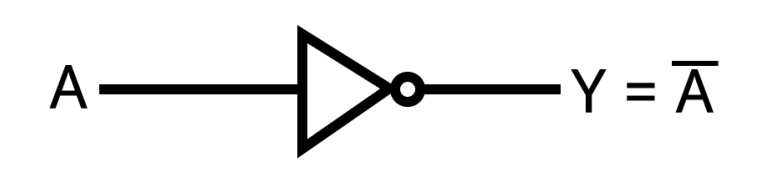
NOT 게이트
- A의 값을 부정. 1일 때 0으로, 0일 때 1로 부정하여 논리부정이라고 한다.
- NOT A 또는 A’ 로 표시
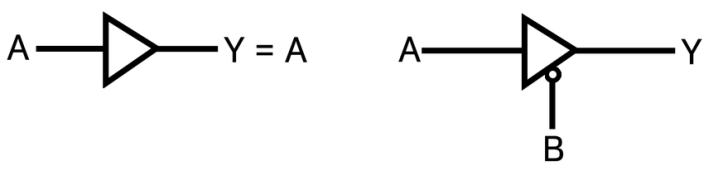
NAND 게이트
- A와 B가 모두 1이 아닐 때 1
- 두 경우를 곱한것의 반대와 같아서 부정논리곱이라고 한다.
- A NAND B 또는 (A・B)’ 또는 (AB)’ 로 표시
| A |
B |
NAND |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
NOR 게이트
- A와 B 둘 중 하나라도 1일 때 0
- 두 경우를 더한 것의 반대와 같아서 부정논리합이라고 한다.
- A NOR B 또는 (A+B)’ 로 표시

| A |
B |
NOR |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
XOR 게이트
- A와 B 가 서로 다를 때 1
- 서로 다른 경우(배타) 더한 것과 같아서 배타적 논리합이라고 한다.
- A XOR B 또는 A⨁B 로 표시

| A |
B |
XOR |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
XNOR 게이트
- A와 B 가 서로 같을 때 1
- 서로 다른 경우(배타) 더한 것의 반대와 같아서 배타적 부정논리합이라고 한다.
- A XNOR B 또는 A⦿B 로 표시

| A |
B |
XNOR |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |








